High-Order Meshes

High-order (curved) meshes appear in many applications, e.g. due to curved material interfaces or due to mesh motion in simulations with moving meshes (for example, ALE methods).

The use of high-order geometry representation can lead to better feature resolution, improved symmetry preservation, better solution adaptivity and increased robustness for problems where the mesh is being deformed in time.

The CEED software supports arbitrary order quadrilateral, hexahedral, triangular and tetrahedral meshes, and our team members are developing algorithms for high-order mesh optimization and solution transfer between deformed high-order meshes (remap).

This is an active area of research for our team and we are interested in collaboration.

Unstructured AMR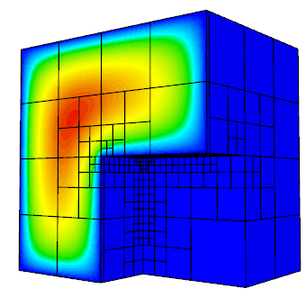

Adaptive Mesh Refinement (AMR) on unstructured grids is an important enabling technology for many applications.

The CEED software supports both conforming AMR on triangular and tetrahedral meshes as well as general non-conforming AMR on quadrilateral and hexahedral meshes. Both approaches work for low-order meshes with no performance penalty and support parallel dynamic load balancing.

One of the distinguishing characteristics of our AMR approach is that it is implemented at the level of the discretization library, decoupled from the physics, so it can easily be incorporated in a variety of applications. We support spaces in the whole de Rham complex, as well as AMR on high-order meshes.

CEED scientists are working on practical error indicators and physics-conservative AMR interpolations to meet application needs.

This is an active area of research for our team and we are interested in collaboration.