Efficient High-Order Operator Format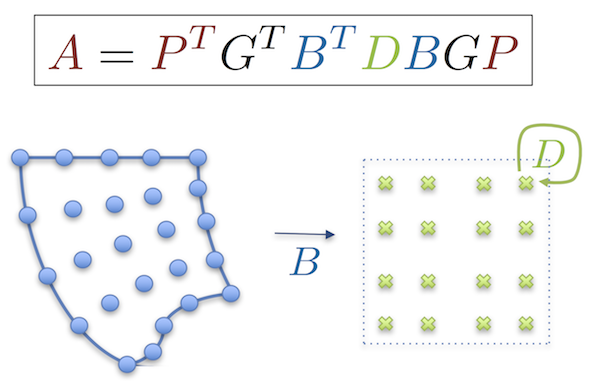

While a global (parallel) sparse matrix is a good representation of a PDE operator discretized with low-order elements, a global parallel matrix is a poor choice when discretizing with high-order elements, due to the large cost of both the memory transfer and floating point operations.

CEED is developing an alternative operator format, based on the CEED low-level API, that allows efficient operator evaluation that is optimal in memory and nearly-optimal in FLOPs cost.

This is an active area of research for our team and we are interested in collaboration.

Stay tuned for more details...

General Interpolation of Solution Field Values

Particle tracking, grid-to-grid transfer and data analysis are typical operations that require off-grid function evaluation.

CEED is developing a scalable interpolation routine for arbitrary-order hexahedral elements that uses a hash table to rapidly identify candidate elements/processors that might contain the point in question, followed by a Newton iteration to find the point in the reference domain.

The iteration is based on minimization, rather than root-finding, which is advantageous when the interpolation point is on or near an element boundary where high-order interpolants tend to exhibit rapid variation.

This is an active area of research for our team and we are interested in collaboration.

Stay tuned for more details...