CEED APIs

CEED is building on the efforts of the Nek5000, MFEM, MAGMA, OCCA and PETSc projects to develop application program interfaces (APIs), both at high-level and at low-level. Multiple APIs are necessary to enable application to take advantage of CEED-developed high-order technologies at the level they are comfortable with. In addition, our high-level API will call internally low-level API functionality.

Low level API

The CEED low-level API, libCEED operates with the foundational components of finite element operators, described by the following decomposition:

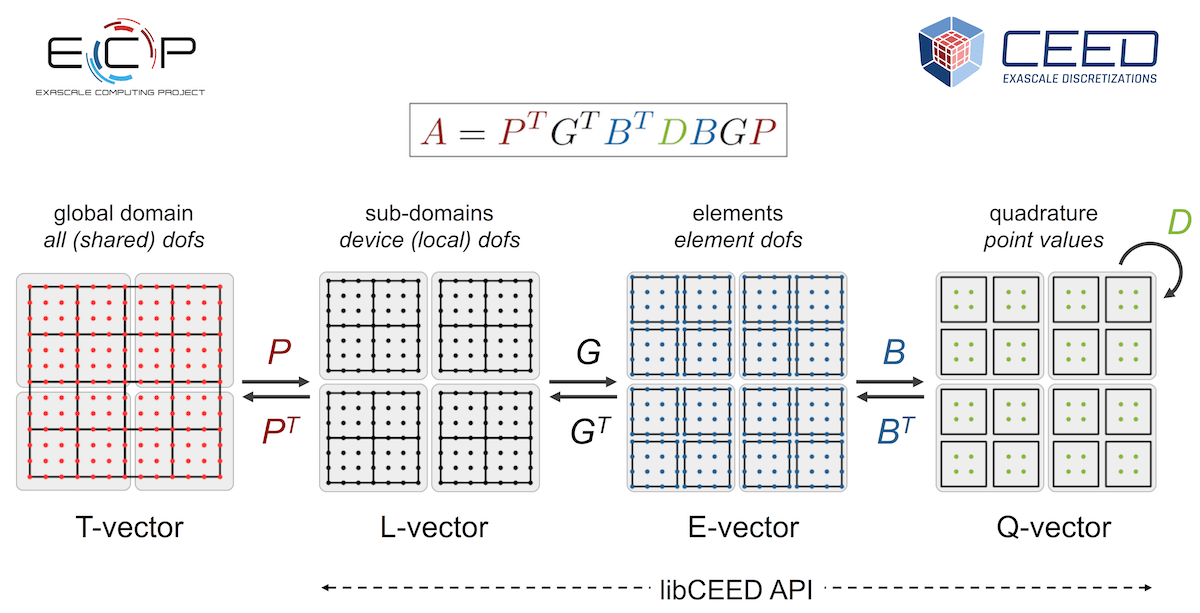
To achieve high-performance, it is critical to take advantage of the tensor-product structure of both the finite element basis and the quadrature rule to efficiently apply the action of $B$ without necessarily computing its entries. This is generally know as sum factorization. In the case where we precompute and store the $D$ matrix, we call the algorithm partial assembly.

Since libCEED is based on a common operator description at algebraic level, it can also be used as the foundation for an efficient high-order operator format.

For more information of the CEED low level API see the libCEED page.

High level API

At a higher level of abstraction, CEED provides a high-level API to applications through the MFEM and Nek codes.

The CEED high-level API operates with global discretization concepts, specifying a global mesh, finite element spaces and PDE operators to be discretized with the point-wise physics representing the coefficients in these operators.

Given such inputs, CEED provides efficient discretization and evaluation of the requested operators, without the need for the application to be concerned with element-level operations. Internally, the high-level API relies on CEED's low-level API described below.

The global perspective also allows CEED to provide general unstructured adaptive mesh refinement support, with minimal impact in the application code.