Finite Element Thrust 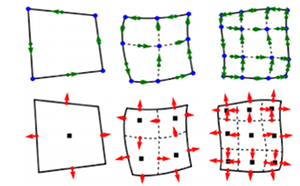
The goal of CEED's Finite Element (FE) thrust, led by Veselin Dobrev from Lawrence Livermore National Laboratory, is to continue to improve the state-of-the-art spectral element/high-order finite element algorithms and kernels in the CEED software targeting exascale architectures.
Why High-Order Finite Elements?
Efficient exploitation of exascale architectures requires a rethink of the numerical algorithms used in large-scale scientific applications. These architectures favor algorithms that expose ultra-fine-grain parallelism and maximize the ratio of floating-point operations to energy-intensive data movement.
Many large-scale applications employ unstructured finite element discretization methods, where practical efficiency is measured by the accuracy achieved per unit computational time. One of the few viable approaches to achieve high performance in this case is to use matrix-free high-order finite element methods, since these methods can both increase the accuracy and/or lower the computational time due to reduced data motion.
To achieve this efficiency, high-order methods use mesh elements that are mapped from canonical reference elements (hexes, wedges, pyramids, tetrahedra) and exploit, where possible, the tensor-product structure of the canonical mesh elements and finite element spaces. Through matrix-free partial assembly, the use of canonical reference elements enables substantial cache efficiency and minimizes extraneous data movement in comparison to traditional low-order approaches.
High-Order Benchmarks and Miniapps
The FE thrust works closely with the Applications and Hardware thrusts on the development of CEED benchmarks and miniapps, and coordinates the project software activities with the Software thrust.
Ecosystem for High-Order Applications
In addition to performance improvements, the FE thrust is focusing on community-wide challenges that are necessary for establishing a full-fledged high-order application software ecosystem.
These efforts include research and development in the following areas: