CEED Miniapps
CEED is developing a variety of miniapps encapsulating key physics and numerical kernels of high-order applications. The miniapps are designed to be used in a variety of co-design activities with ECP vendors, software technologies projects as well as external partners.
CEED's current miniapps are documented below and can be found on GitHub. Please contact the CEED team if you have any questions.
Nekbone
Nekbone solves a standard Poisson equation using a conjugate gradient iteration with a simple or spectral element multigrid preconditioner on a block or linear geometry.
It exposes the principal computational kernel to reveal the essential elements of the algorithmic-architectural coupling that is pertinent to Nek5000, relevant to large eddy simulation (LES) and direct numerical simulation (DNS) of turbulence in complex domains.
Nekbone-3.1 was released in Oct 2013 as part of the CESAR co-design center.
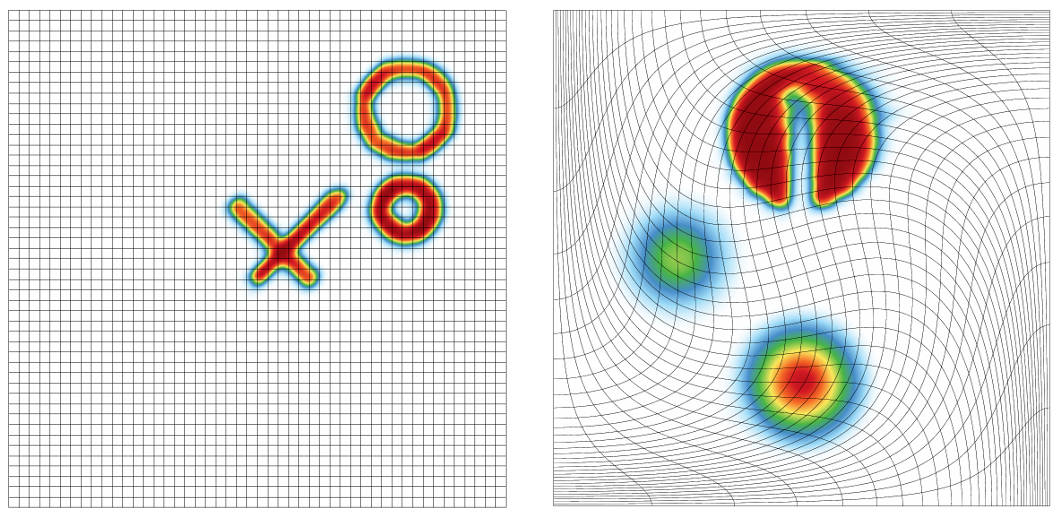
Laghos
Laghos solves the time-dependent Euler equation of compressible gas dynamics in a moving Lagrangian frame using high-order finite element spatial discretization and explicit high-order time-stepping.
It captures the basic structure of many other compressible shock hydrocodes, including the BLAST code at Lawrence Livermore National Laboratory. The miniapp is build on top of a general discretization library, MFEM, thus separating the pointwise physics from finite element and meshing concerns.
Computational motives in Laghos include the following:
- Support for moving (high-order) unstructured 2D and 3D meshes.
- Continuous and discontinuous high-order finite element discretization spaces of runtime-specified order.
- Explicit time-stepping loop with a variety of time integrator options. Laghos supports Runge-Kutta ODE solvers of orders 1, 2, 3, 4 and 6.
- Full and partial assembly options for deriving and solving the resulting ODE systems.
- Point-wise definition of mesh size, time-step estimate and artificial viscosity coefficient.
- Domain-decomposed MPI parallelism.
- Optional in-situ visualization with GLVis and data output for visualization / data analysis with VisIt.
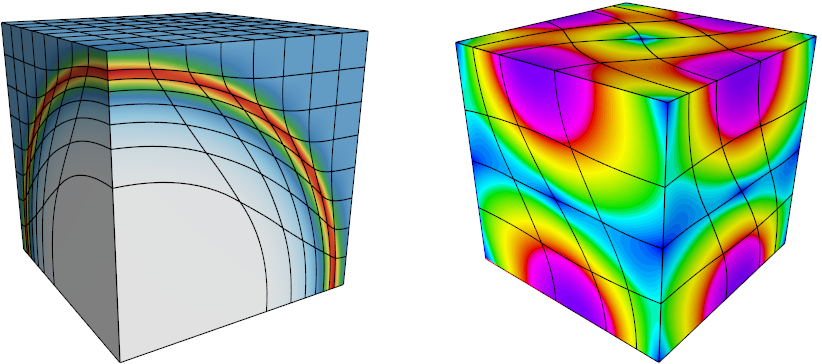
Remhos New
Remhos solves the pure advection equations that are used to perform conservative and monotonic DG advection-based discontinuous field interpolation (remap).
It captures the basic structure of the Eulerian phase in many Arbitrary-Lagrangian Eulerian (ALE) simulations, including the BLAST code at Lawrence Livermore National Laboratory. The miniapp is build on top of a general discretization library, MFEM, thus separating the pointwise physics from finite element and meshing concerns.
Computational motives in Remhos include the following:
- Support for unstructured high-order meshes, in 2D and 3D, with quadrilateral and hexahedral elements.
- Discontinuous high-order finite element discretization spaces of runtime-specified order.
- State-of-the-art algorithms for high-order monotonicity (including positivity preservation and oscillation control).
- Explicit time-stepping loop with a variety of time integrator options. Remhos supports Runge-Kutta ODE solvers of orders 1, 2, 3, 4 and 6.
- Full and partial assembly options for deriving and solving the resulting ODE systems.
- Supports for both transport and remap execution modes, which result in slightly different algebraic operators.
- Domain-decomposed MPI parallelism.
- Optional in-situ visualization with GLVis and data output for visualization / data analysis with VisIt.
NekCEM CEEDling
NekCEM CEEDling is a NekCEM miniapp, solving the time-domain Maxwell equations for electromagnetic systems. It allows software and hardware developers to understand the basic structure and computational costs of NekCEM over a broad spectrum of architectures ranging from software-based simulators running at one ten-thousandth the speed of current processors to exascale platforms running millions of times faster than single-core platforms.
NekCEM provides flexibility to adapt new programming approaches for scalability and performance studies on a variety of platforms without having to understand all the features of NekCEM, currently supporting CPU/GPU runs.
HPGMG-FE
The High-Performance Geometric Multigrid Finite Element benchmark is a Full Multigrid solver for a third order accurate finite element discretization of an elliptic operator on mapped grids. The benchmark is designed to give a picture of the "performance spectrum" across a range of problem sizes and thus solution time, thereby giving a clear picture of both weak and strong scaling concerns.
For details, see the HPGMG website.
MFEM Example Codes
The MFEM distribution includes a large number of simple example codes that can be viewed as simple miniapps for model high-order physics:
- Example 1: nodal H1 FEM for the Laplace problem,
- Example 2: vector FEM for linear elasticity,
- Example 3: Nedelec H(curl) FEM for the definite Maxwell problem,
- Example 4: Raviart-Thomas H(div) FEM for the grad-div problem,
- Example 5: mixed pressure-velocity FEM for the Darcy problem,
- Example 6: non-conforming adaptive mesh refinement (AMR) for the Laplace problem,
- Example 7: Laplace problem on a surface (the unit sphere),
- Example 8: Discontinuous Petrov-Galerkin (DPG) for the Laplace problem,
- Example 9: Discontinuous Galerkin (DG) time-dependent advection,
- Example 10: time-dependent implicit nonlinear elasticity,
- Example 11: parallel Laplace eigensolver,
- Example 12: parallel linear elasticity eigensolver,
- Example 13: parallel Maxwell eigensolver,
- Example 14: Discontinuous Galerkin (DG) for the Laplace problem,
- Example 15: dynamic AMR for Laplace with prescribed time-dependent source,
- Example 16: time-dependent nonlinear heat equation,
- Example 17: Discontinuous Galerkin (DG) for linear elasticity,
- Example 18: Discontinuous Galerkin (DG) for the Euler equations,
- Example 19: incompressible nonlinear elasticity.
Most of the examples have a serial and a parallel version, illustrating the ease of transition and the minimal code changes between the two.
Of particular relevance to CEED is the HPC versions of the example codes that use a set of templated classes to efficiently implement high-order operator evaluation.